БГПУ. Кафедра методики преподавания физики

§ 4. Эмпирический и теоретический подходы к конструированию лабораторного эксперимента по элементарному курсу физики

   Проведение поэлементного анализа логически завершенного раздела курса физики и систематизация полученного материала позволяет выделить в нем не только рассмотренный выше ряд видов знаний (величины, законы, теории и т.д.), но и построить некоторый перечень сюжетов, которые могут лечь в основу последующего конструирования лабораторных установок, выполняемых на этих установках лабораторных работ, а также системы физических задач.
   Рассмотрим для примера ряд сюжетов по элементарному курсу механики, на базе которых в рамках спецпрактикума нами осуществлялось обучение студентов физического факультета БГПУ принципам конструирования системы школьного лабораторного эксперимента.

Сюжеты для конструирования лабораторных установок по
элементарному курсу механики

Словесное описание сюжета	Схематический рисунок	Уравнение,описывающее сюжет
Равномерное движение тела (бруска, тележки, шарика) по горизонтальной (или слегка наклоненной для компенсации силы трения) поверхности.		v=S/t
Равномерное вращение тела по окружности в горизонтальной плоскости		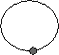w=a/t
Равноускоренное движение тела (бруска, тележки, шарика) по наклонной плоскости.		a=2*S²/t
Равномерное движение связанных, уравновешивающих друг друга грузов в вертикальной плоскости.		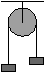v=S/t
Равноускоренное движение связанных, неуравновешивающих друг друга грузов в вертикальной плоскости.		mg/(m+2M)=2*S/t²
Равноускоренное движение тела по горизонтальной поверхности (без учета силы трения) под действием падающего груза.		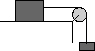mg/(m+M)=2S/t²
Равноускоренное движение тела по горизонтальной поверхности (с учетом силы трения) под действием падающего груза		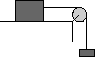(m-мM)g/(m+M)=2*S/t²
Равноускоренное движение тела по наклонной плоскости (без учета силы трения) под действием падающего груза.		\|(Msin(a)-m)g/(m+M)\|=2*S/t²
Равноускоренное движение тела по наклонной плоскости (с учетом силы трения) под действием падающего груза.		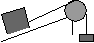\|(M(sin(a)-мcos(a))-m)g/(m+M)\|=2S/t²
Подъем тела на некоторую высоту с помощью шероховатой наклонной плоскости.		n=1/(м*ctg(a)+1)
Равномерное движение бруска по горизонтальной поверхности под действием горизонтально приложенной силы.		F=F_тр=мmg
Равномерное движение бруска по горизонтальной поверхности под действием силы, направленной под углом к горизонту		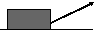F=мmg/(sin(a)+м*cos(a))
Равномерное движение бруска вверх вдоль наклонной плоскости под действием приложенной к нему силы.		F=mg(sin(a)+м*cos(a))
Равномерное скольжение бруска вниз по наклонной плоскости.		м=tg(a)
Движение бруска по горизонтальной поверхности под действием силы упругости, уменьшающейся по линейному закону.		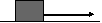kx2/2=мmgS
Равномерное вращение тела по окружности в горизонтальной плоскости. Тело привязано к нити, пропущенной через трубку. Второй конец нити привязан к пружине динамометра или к другому телу. (Провисание нити мало).		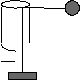F=4п²Rv²m
Равномерное вращение тела по окружности в горизонтальной плоскости. Тело привязано к нити, другой конец которой неподвижно закреплен. Нить при движении описывает коническую поверхность.		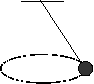mgtg(a)=m(2пvR)²/R
Упругий центральный удар шаров, подвешенных на нитях.		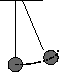Mv²/2=mu₁²/2+Mu₂²/2 Mv=mu₁+Mu₂
Неупругий центральный удар шаров, подвешенных на нитях.		2gHm₁²/(m₁+m₂)²=2g*h
Выстрел из баллистического пистолета под углом к горизонту.		(gx²/2v₀²cos²(a))-xtg(a)+y=0
Выстрел из баллистического пистолета в брусок, подвешенный на нитях. Снаряд застревает в бруске.		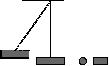m²v²/(m+M)²=g*S²/L
Растяжение пружины с помощью подвешиваемых к ней грузов.		F=f(x)
Колебания пружинного маятника.
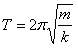Колебания нитяного маятника.
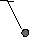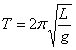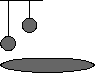
Падение двух тел с разных высот на равномерно вращающийся диск.

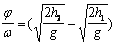   Естественно, перечень сюжетов, которые могут лечь в основу для конструирования лабораторных установок, на этом не ограничивается. Наряду с приведенными, можно рассматривать сюжеты, характеризующие состояние тела в движущемся вертикально с ускорением лифте; систему статических сюжетов: силы упругости, возникающие в балках, укосах, равновесие рычагов, плоских пластин и объемных тел; преобразования энергии, в частности, взаимообратные переходы потенциальной и кинетической, механической и электрической энергии.
   Остановимся на примере сюжета, связанного с движением тела по наклонной плоскости и сконструируем на его основе серию экспериментальных заданий, которые можно было бы положить в основу различного типа инструкций по выполнению лабораторных работ.
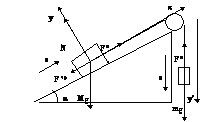
   Конкретизируем сюжет: деревянный брусок находится на деревянной поверхности, расположенной под углом к горизонту.

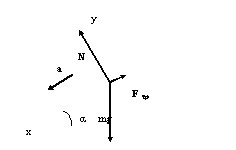
При отсутствии силы тяги со стороны какого-то другого тела, на брусок действуют сила тяжести mg, сила реакции со стороны опоры N, сила трения F_тр. В общем случае, эти силы сообщают бруску ускорение a, направленное вниз вдоль наклонной плоскости:

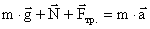
   Или, в проекциях на координатные оси: x: mg*sin(a)-F_тр=ma y:-mg*cos(a)+N=0 где: F_тр=м*N =м*mg*cos(a)
   Решая совместно эти уравнения, получаем: mg*sin(a)-м*mg*cos(a)=ma
   Окончательно:g*(sin(a)-м*cos(a))=a
   Полученное уравнение описывает явление движения тела (в нашем случае - бруска) по наклонной плоскости, если на это тело не действует сила тяги со стороны другого тела.
   Для рассмотренного сюжета могут быть сформулированы следующие экспериментальные задания.

Основание для формулировки экспериментальных заданий	Примеры экспериментальных заданий для данного основания
Брусок равномерно скользит вниз вдоль наклонной плоскости. Его ускорение равно нулю. Тогда: gsin(a)-мcos(a)=0;sin(a)=мcos(a);м=tg(a)	Определить коэффициент трения скольжения дерева по дереву, не используя для этого динамометра.
Брусок равномерно скользит по плоскости, расположенной под углом к горизонту, равным нулю. При этом сила трения скомпенсирована силой тяги, приложенной параллельно плоскости. a=0,Fтр =мmg	1. Определить коэффициент трения скольжения дерева по дереву. 2. Определить силу, которую необходимо приложить к телу, чтобы равномерно перемещать его по горизонтальной поверхности.
Брусок равномерно скользит вверх вдоль наклонной плоскости. При этом плоскость расположена под таким углом к горизонту, что,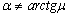 Fтр=mg(sin(a)-мcos(a)),где:sin(a)=h/L.	Определить значение силы тяги, которую следует приложить к бруску, чтобы равномерно поднимать его по наклонной плоскости, расположенной под углом к горизонту.
Брусок равноускоренно движется вниз вдоль наклонной плоскости. При этом м>0;a> arctg(м);м=tg(a₀);a=g(sin(a)-tg(a₀)cos(a)).	Определить ускорение движения бруска, соскальзывающего с наклонной плоскости.
Тот же случай, что и предыдущий, но ускорение движения бруска выражается через другие кинематические величины, непосредственно измеряемые в эксперименте - перемещение S и время t:	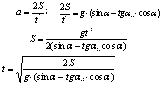1. Определить перемещение бруска, скатывающегося с наклонной плоскости за заданное время. 2. Определить, за какое время брусок совершит заданное перемещение?

   Аналогичным образом запишутся уравнения и будут сформулированы экспериментальные задания для случая движения по плоскости не бруска, а легкоподвижной тележки.
   При этом легкоподвижная тележка может быть изготовлена из того же бруска путем прикрепления к нему колес. Разница будет заключаться в том, что в исходном уравнении, описывающем этот процесс, коэффициент трения скольжения можно будет принять равным нулю: = 0.
   Существенно, что для выполнения всех названных заданий требуется одна и та же экспериментальная установка.
   Очень схожей является и теоретическая часть лабораторных работ, построенных на основе этих экспериментальных заданий.
   Однако, логика рассуждений, последовательность действий при выполнении практической части работы несколько отличны друг от друга в каждом из вариантов работы.
   Добавим в экспериментальную установку еще один груз и опишем движение связанных тел.
   Как и в предыдущем случае, рассмотрим для этого силы, действующие на тела и запишем второй закон Ньютона для каждого из этих тел. Нить будем считать нерастяжимой, а ее массу равной нулю.
   Пусть, для определенности, брусок движется вверх вдоль наклонной плоскости.

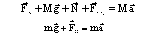
   В проекциях на выбранные направления уравнения имеют вид:
   x:F_н-Mgsin(a)-F_тр=Ma, где F_тр=N
   y:N-Mgcos(a)=0
   y`:mg-F_н=ma
   Решая уравнения совместно, имеем: (M+m)a=(m-M(sin(a)+cos(a)))g.
   К перечисленному выше перечню экспериментальных заданий, для измененного таким образом сюжета, добавятся, например, такие задания:
   Определить массу груза m, который необходимо прикрепить к нити, переброшенной через блок и связанной с бруском массы М, чтобы брусок:
   а) двигался с заданным ускорением;
   б) совершал заданное перемещение за заданное время.
   Для тележки, движущейся по наклонной плоскости с пренебрежимо малым трением в соответствии с таким же сюжетом, уравнение будет иметь более простой вид: (M+m)a=(m-Msin(a))g.
   Формулировки же экспериментальных заданий практически не изменятся.
   Аналогичным образом можно выявить перечень и сформулировать экспериментальные задания для любых, как рассмотренных, так и не рассмотренных выше сюжетов. При этом формулировать задания можно как произвольным образом, так и соотнося формулировки с выделенными выше видами экспериментальных заданий.
   Конструируя содержание лабораторного эксперимента, учитель должен решать множество общепедагогических и методических задач.
   В частности, учителю необходимо обеспечить самостоятельность выполнения работ каждым учеником.
   Самостоятельность должна обеспечиваться не репрессивными методами, не усилением надзора над процессом выполнения работ, а естественным образом, в идеале таким, чтобы вообще была снята потребность в контроле за самостоятельностью выполнения работ.
   При этом уровень и содержание экспериментальных заданий должны соответствовать уровню развития и подготовки каждого отдельного ученика.
   Являясь заданиями развивающими, экспериментальные задания должны быть посильными при их выполнении. В идеале, сказанное означает: сколько учеников, столько и заданий.
   В то же время, экспериментальные задания, предъявляемые ученикам, не могут быть произвольными. Во-первых, поскольку существует несколько видов значительно отличающихся по методологии видов экспериментальных работ, постольку естественным было бы представить в системе лабораторного эксперимента все его виды. Во-вторых, поскольку внутри каждого вида эксперимента существует несколько методов его реализации, постольку крайне желательно, чтобы ученик при выполнении различных работ познакомился с этими методами проведения эксперимента.
   Рассмотрим, каким может быть принцип отбора заданий при конструировании содержания учебного лабораторного эксперимента по элементарному курсу физики.
   Для наглядности этот принцип имеет смысл представить в виде схемы.
   Схема строится путем формально-логического анализа сюжета, лежащего в основе экспериментальной установки.
   Таким образом, принцип отбора заданий для лабораторного эксперимента пока не является личностно ориентированным и не содержит в себе собственно педагогической составляющей. Эта составляющая должна быть наложена на отобранные задания в ходе их дальнейшего педагогического анализа.

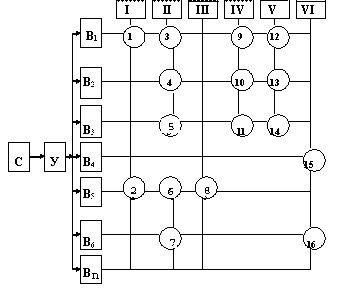Рис. 4.1. Формально-логическая схема отбора заданий для
лабораторного эксперимента по абстрактному сюжету.
   С - сюжет, являющийся основой для конструирования экспериментальной установки.
   У - уравнение, описывающее данный сюжет.
   В1 - ВN - физические величины, входящие в уравнение У.
   I - VI - основные виды экспериментальных заданий:
   I - Изучение физических явлений, процессов, состояний физических объектов.
   II - Введение производной физической величины.
   III - Определение численного значения физической величины.
   IV - Определение численного значения физической постоянной.
   V - Исследование зависимостей между физическими величинами.
   VI - Изготовление или изучение прибора, механизма.
   1-16 - Экспериментальные задания для учащихся, сформулированные в соответствии с основными видами экспериментальных заданий в приложении к анализируемому сюжету.
   Рассмотрим на примере, как представленная схема может быть использована для отбора и формулировки экспериментальных заданий, которые лягут в дальнейшем в основу лабораторных работ по курсу элементарной механики.
   Описание сюжета:
   Два груза одинаковой массы M1 = M2 = M, связаны легкой и нерастяжимой нитью, которая переброшена через неподвижный блок.
   Масса блока и трение в его оси малы.
   На один из грузов положили перегрузок массой m, после чего вся система начала равноускоренно двигаться и за время t каждый из грузов совершил перемещение S.
   Уравнение, описывающее данный сюжет:mg/(2M+m)=2S/t² .
   Величины, входящие в уравнение: m, M, g, S, t.
   Схема построения экспериментальных заданий по данному сюжету:

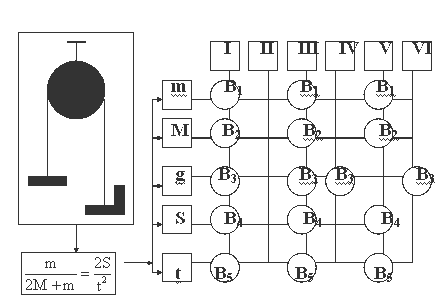Рис. 4.2. Формально-логическая схема отбора заданий для
лабораторного эксперимента по конкретному сюжету.

Примеры экспериментальных заданий, формулируемых с
использованием приведенной схемы:
1 (I - B1-B5)
   Изучить характер движения неуравновешивающих друг друга грузов, связанных нитью, переброшенной через неподвижный блок.
2 (III - B1)
   Определить массу перегрузка m, который необходимо положить на один из уравновешивающих друг друга грузов, чтобы этот груз за t с совершил перемещение S см.
3 (III - B2)
   Определить массу одного из уравновешивающих друг друга грузов M, на котором лежит перегрузок известной массы m г, если за t с груз совершает перемещение S см.
4 (III - B4)
   Определить перемещение S, которое совершит один из уравновешивающих друг друга грузов массы M за время t, если на этот груз положить перегрузок массой m.
5 (III - B5)
   Определить время t, за которое один из уравновешивающих друг друга грузов массы M совершит перемещение S, если на этот груз положить перегрузок массой m.
6 (IV - B3)
   С помощью неуравновешивающих друг друга грузов, связанных нитью, переброшенной через неподвижный блок, определить численное значение ускорения свободного падения g.
7 (V - B4-B5)
   Исследовать зависимость между перемещением S и временем t движения тела с помощью неуравновешивающих друг друга грузов, связанных нитью, переброшенной через неподвижный блок.
8 (V - B4-B1)
   Исследовать зависимость перемещения S, совершаемого грузом с перегрузком за одно и то же время, от массы перегрузка m.
9 (V - B5-B1)
   Исследовать зависимость времени t одного и того же перемещения груза с перегрузком от массы перегрузка m.
10 (VI - B3)
   Имея в своем распоряжении неподвижный блок, легкую и нерастяжимую нить, набор грузов, линейку и секундомер, изготовьте установку, с помощью которой можно было бы определить численное значение ускорения свободного падения g. Произведите необходимые измерения и расчеты. Изучите, как работает предложенная вами установка, придумайте как можно больше способов ее практического применения и проиллюстрируйте некоторые из этих способов.
   Естественно, что не все задания, полученные путем формально-логического анализа сюжета, лежащего в основе экспериментальной установки, будут в дальнейшем реализованы в учебном процессе.
   Однако, значительное их количество позволит учителю представить в практикуме все типы экспериментальных заданий, составить индивидуальные варианты работ для всех учащихся класса.