6. Цели решения задач
Особое внимание должно быть обращено на постановку цели, которая преследуется при решении задач.
Рассмотрим отдельные цели, возможные при решении школьных физических задач.
Решение задач с целью формирования физических понятий
Например, в разделе "кинематика" курса механики одними из основных являются понятия пути и перемещения.
Учащиеся достаточно хорошо понимают разницу между ними, но, тем не менее, при решении некоторых задач путают их. Особенно это относится к случаю, когда тело движется вдоль одной прямой, но в какой-то момент времени меняет направление своего движения.
Чтобы иметь полное представление о той или иной величине, надо знать не только ее особенные, но и отличительные черты.
Для демонстрации отличия понятий пути и перемещения можно предложить учащимся следующую задачу:
Тело, имеющее скорость 10 м/с, с некоторого момента начинает двигаться с ускорением -2 м/с .
Какой путь пройдет это тело за первые 6 секунд, начиная с момента начала торможения?
Обычно эта задача решается сразу по формуле: S = v
0 * t + a * t
2/2 , что, естественно, не верно, т.к. ищется в этом случае не путь, а перемещение тела.
Чтобы навести решающего на мысль об ошибочности решения, можно предложить ему рассчитать путь, пройденный телом за 8 секунд, считая с момента начала замедленного движения.
Ответ получается меньшим, чем в первом случае, что противоречит как здравому смыслу, так и определению пути.
Ошибка в подходе к решению задачи связана с барьером прошлого опыта решения задач и кажущейся легкостью решения (имеется расчетная формула и все необходимые для подстановки в нее данные).
Более детальный анализ сюжета задачи и методичное следование пунктам алгоритмического предписания по решению кинематических задач позволяют как найти искомый путь, так и выяснить, в чем состоит различие между понятиями пути и перемещения.
Параллельно с этим обращается внимание на необходимость следования алгоритмическому предписанию по решению задач, даже несмотря на кажущуюся вначале их простоту.
Решение задач с целью формирования представлений о границах применимости формул, законов
В курсе кинематики средней школы изучается равнопеременное движение.
Это движение описывается выражениями вида:
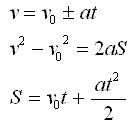
У учащихся часто складывается неверное представление об универсальном характере действия этих формул в случае неравномерного движения.
В связи с этим возникают трудности в объяснении разных ответов при использовании непротиворечивых формул при решении следующей задачи:
Троллейбус, имевший скорость 10 м/с, начал тормозить.
При каком ускорении он пройдет до полной остановки 8 м за 2 с?
Решение:
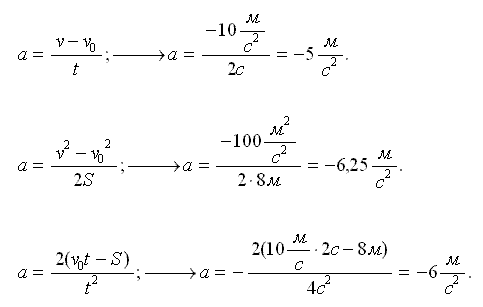
Суть ответа сводится к тому, что если считать движение равнозамедленным, то одно из данных задачи является лишним и неверным. В случае такого движения, подобного соотношения данных быть не может.
Но возможен и такой вариант, когда все данные являются верными, но тогда движение должно быть неравнозамедленным и ни одна из использованных формул для его описания применена быть не может.
Анализ подобной задачи позволит лучше, чем где-либо показать границы применимости используемых при решении задач формул.
Решение задач с целью демонстрации рациональных и нерациональных способов решения, а так же необходимости использования предписаний алгоритмического типа
Гораздо большую пользу принесет учащимся решение одной задачи несколькими способами, нежели решение большого количества задач одним способом. При этом среди разных способов можно выделить способы как рациональные, так и нерациональные.
Часто рациональные способы не используются учащимися в силу тех или иных особенностей мышления, привычки и т.д. Перед учащимися возникают своеобразные психологические барьеры, перешагнув через которые они дальше без особого труда могут решить предлагаемую задачу способом более рациональным и легким, нежели способом стандартным или кажущимся легким на первый взгляд.
Приведем пример задачи:
Из гондолы воздушного шара, поднимающегося вертикально вверх с постоянной скоростью 10 м/с, выпал предмет, который упал на Землю через 5 с.
На какой высоте находился шар в тот момент, когда предмет коснулся Земли?
Очень часто такую задачу решают поэтапно:
1) Находят время движения выпавшего предмета вверх:
2) Находят время падения предмета до того места, откуда он выпал из гондолы шара: t
2 = t
1 = 1с и скорость в этой точке.
v = 10м/с и направлена вертикально вниз.
3) Находят перемещение предмета за оставшиеся 3с, т.е. высоту на которой находился шар в момент отделения от него предмета
h
1=75м.
4) Находят перемещение шара за 5с.
h
2 = v
0 * t ; h
2 =50м.
5) Находят общую высоту как H = h
1 + h
2 ;
H = 125м.
Но эта же задача может быть решена с помощью координатного метода.
Записываются уравнения движения шара и тела в системе отсчета, связанного с Землей:
По условию задачи:
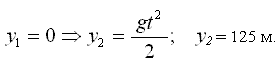
В итоге оказалась невостребованной скорость шара. Уже отсюда вытекает, что хотя первый способ и кажется физически более понятным и простым, на самом деле он становится неприемлемым, как только из условия задачи будет исключена скорость шара.
Приведенные решения позволяют показать преимущества общего подхода к решению кинематических задач.
Но задача имеет и более рациональное решение.
Если связать систему отсчета с движущимся шаром и ось у направить вертикально вниз, то уравнение движения тела запишется: y = g * t
2/2 ; у=125м.
Такое решение редко приводится учащимися в силу того, что они "привыкли" связывать систему отсчета с Землей, каким-то неподвижным телом.
Решение задач, направленное на демонстрацию ошибочности использования наиболее очевидных формул, законов
Задача
Поезд первую половину пути шел со скоростью 30км/ч, а вторую половину пути - со скоростью 50км/ч.
Какова средняя скорость движения поезда на всем пути?
Типичный ответ - 40км/ч, который сразу дают ученики, связан с внешним, хотя и очень отдаленным сходством предлагаемой задачи с задачами на отыскание среднего арифметического.
Эта кажущаяся очевидность и заставляет учеников "забыть" хорошо известную им определительную формулу для вычисления средней скорости: v
ср = L
весь/t
все .
Чтобы навести учащихся на мысль об ошибочности их ответа целесообразно сразу же привести задачу с теми же данными, но слегка измененным сюжетом:
Поезд первую половину времени шел со скоростью 30км/ч, а вторую половину времени - со скоростью 50км/ч.
Какова средняя скорость поезда на всем пути движения?
И только после того, как учащиеся задумаются над вопросом - в чем разница между задачами, можно их решить, акцентировав внимание на совершенно одинаковом подходе к решению и необходимости знания всего лишь одной определительной формулы для решения разных задач на нахождение средней скорости.
Особо еще раз следует отметить, что для достижения цели,
задачи должны предлагаться с очень похожим сюжетом, с одинаковыми числовыми значениями и обязательно в паре - одна за другой.
Решение задач для закрепления теоретических выводов
Известно затруднение в решении ряда задач на колебательные системы, вызванное некорректностью, либо поспешностью выяснения физического смысла коэффициента пропорциональности "k" в дифференциальном уравнении, описывающем гармонические механические колебания:
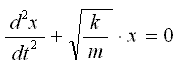
Это задачи, аналогичные такой:
В жидкости плавает ареометр. Его выводят из положения равновесия путем легкого погружения в жидкость, после чего отпускают.
Найти период колебаний ареометра.
Сопротивлением движению пренебречь.
При изучении темы "Механические колебания" один из акцентов должен быть сделан на том, что поскольку формула
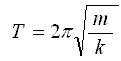
получается непосредственно при решении уравнения, описывающего гармонические механические колебания любых механических систем, она является основной формулой для расчета периода, а все остальные формулы, в том числе и формула для расчета периода колебаний математического маятника
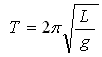
, могут быть получены как ее частные случаи.
При этом последовательность действий по решению задач данного вида будет такой:
Ставится вопрос: является ли рассматриваемое движение гармоническими колебаниями, т.е. пропорциональна ли сила, выводящая тело из положения равновесия, смещению и направлена ли эта сила к положению равновесия?
Если при анализе выяснится, что результирующая сила, действующая на тело, не пропорциональна смещению, то формула
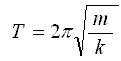
не подходит для расчета периода колебаний и задача в рамках курса физики средней школы является нерешаемой.
Если же, наоборот, сила оказывается пропорциональной смещению, то период колебаний будет находиться по этой формуле.
Для нахождения периода достаточно будет подставить в имеющуюся формулу значение коэффициента пропорциональности между силой и смещением, которое получается при количественном анализе задачи.
Таким образом, сложная для учащихся задача может стать обычной стандартной и использоваться в данном случае как упражнение, направленное на закрепление и отработку полученного в теории знания.

